MODULES

Three-Dimensional Droplet Falling Over Thin Liquid Film

Problem Definition:

We present the numerical experiment of a 3-dimensional liquid droplet falling over thin liquid film. This typical test is characterized by the following non-dimensional parameters:




where Do and Uo are the diameter and initial velocity of the droplet, ρ1 and μ1 are the density and dynamic viscosity of heavier fluid, σ is the surface tension coefficient, g is the acceleration due to gravity, h is the film thickness and t is the physical time. Initially the droplet is placed 2.8 diameters above the liquid film with a uniform velocity Uo. The computational domain chosen for this test case is of size 6Do × 6Do × 6Do, which is discretized into 512000 non-uniform hexahedral cells. Top boundary is open to atmosphere while the remaining boundaries are treated as walls. Simulations are performed with We=250, Re=11294, Fr=363 and H=0.116.




Results:

The results are shown in Fig. 4.1. The droplet smoothly impinges on to the liquid film and a crown like shape is also formed, which moves out with time. The simulation outcome is also compared with the published results of Rieber and Frohn [1] and Nikolopoulos et al. [2, 3] and are shown in Fig. 4.2.



Figure 4.1: Iso-surface of volume fraction f = 0.5 for droplet falling over thin liquid film after time t = 2.6, 4.0 and 5.0.



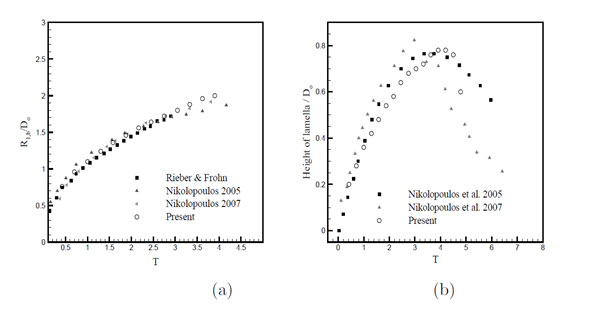
Figure 4.2: Comparison of the radial distance at the bottom of the rim and height of the lamella with the published results [1–3].

References:

[1] Rieber M. and Frohn A. (1999) ‘A numerical study on the mechanism of splashing.’, Int. J. Heat Fluid Flow, vol. 20, p. 455461.

[2] Nikolopoulos N., Theodorakakos A., and Bergeles G. (2005) ‘Normal impingement onto a wall film: a numerical investigation.’, Int. J. Heat Fluid Flow, vol. 26, p. 119132.

[3] Nikolopoulos N., Theodorakakos A., and Bergeles G. (2007) ‘Three-dimensional numerical investigation of a droplet impinging normally onto a wall film.’, Journal of Computational Physics, vol. 225, p. 322341.