MODULES

Conjugate Heat Transfer Of Backward-Facing Step Flow

Problem Definition:

In this problem backward-facing step flow is solved as a conjugate heat transfer, there is some finite thickness of bottom wall and constant temperature is applied at the bottom and upper wall is insulated. The geometry of the problem is shown in Fig. 5.1. In this problem step height is considered to be half of the channel height. Computational domain is divided into 96000 domains, 48000 cells in fluid region and 48000 cells in solid region. Near the walls and near the downstream locations more cells are used. Incompressible and laminar flow is solved combined with energy equation.





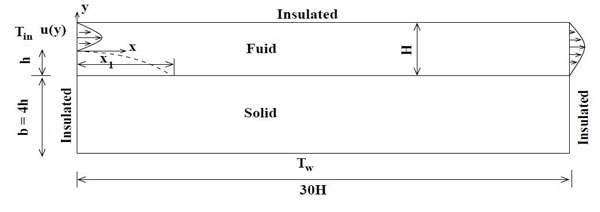
Figure 3.1: Sketch of the conjugate forced convection problem of channel



Results:

Conjugate heat transfer analysis has been done for backward-facing step flow for different conductivity ratio. Temperature contour are shown in Fig. 5.2 for different conductivity ratio. When conductivity ratio is increasing then temperature at interface is increasing and in solid it is approaching towards transient. Temperature variation along the interface is shown in Fig. 5.3 and compared with Ramsak [1]. Variation of interface temperature for different conductivity ratio is compared with literature and found good agreement between both results. When conductivity ratio is 1000 then variation of temperature in solid become transient.



(a) k=1



(b) k=10



(c) k=100



(d) k=1000

Figure 5.2: Effect of k on Isotherms




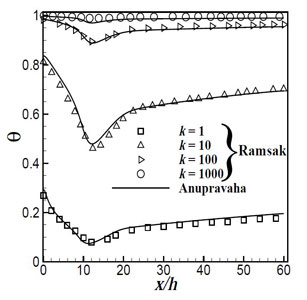
Figure 5.3: Variation of Temperature along interface

References

[1] Ramsak M. (2015) ‘Conjugate heat transfer of backward-facing step flow: A benchmark problem revisited’, International Journal of Heat and Mass Trans-fer, vol. 84, pp. 791–799.