MODULES

Conjugate Forced Convection In A Channel: Half Domain And Sinusoidal Varying Temperature Boundary

Problem Definition:

In this problem conjugate forced convection is studied with sinusoidal longitudinal temperature boundary condition at the external wall of the channel. The geometry of the problem is shown in Fig. 3.1. In this problem, only half channel is solved because of symmetry about y=0.

In this problem solid wall thickness is taken as 0.2m, channel height is 2m and the channel length is 6.3m. This problem is solved for the Peclet number 100 and conductivity ratio is 3. For this problem Peclet number is calculated using average velocity 1 and channel height 1 and conductivity ratio is the ratio of the thermal conductivity of solid to fluid. For solving the problem the computational domain is divided into grids as shown in the Fig. 3.2.

There are 180 uniform grids along the length of the channel and 40 grids are in the perpendicular direction. There are 10 grids in solid with both side clustering and 30 grids are in the fluid with a cluster near the interface as shown in Fig. 3.2. Total 7200 cells are used for the calculation.





Figure 3.1: Sketch of the conjugate forced convection problem of channel



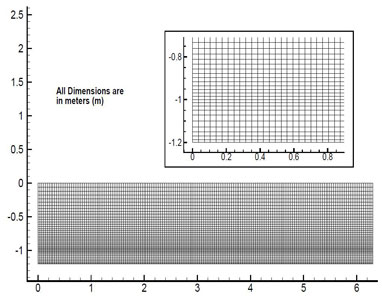
Figure3.2: Meshing of computational domain

Boundary Conditions:





Results:

The inlet velocity is taken as the condition of fully developed flow because here main aim is to solve temperature. Stream-traces are parallel to the channel. Fig. 3.3 shows the isotherms. The temperature boundary condition is sinusoidal longitudinal at the wall of the channel so the isotherms are also like a sinusoidal line. Isotherms are showing the variation of temperature in computational domain. The results obtained from Anupravaha solver is compared with Barletta et al. [38] results. Figure 3.4 shows the comparison of temperature variation along the interface with Barletta et al. [38] results and both results are matching.



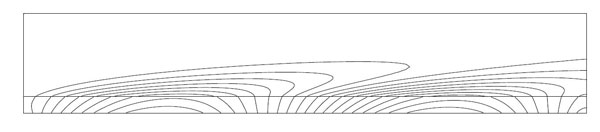
Figure 3.3: Isotherm



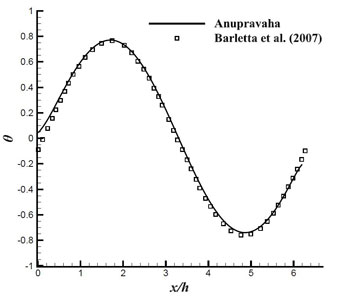
Figure 3.4: Temperature variation along the interface.

References

[1] Barletta A., Di Schio E.R., Comini G., and Agaro P.D. (2008) ‘Conjugate forced convection heat transfer in a plane channel:longitudinally periodic regime’, International Journal of Thermal Sciences, vol. 47, pp. 43–51.