MODULES
×
![]()
Conjugate Forced Convection In A Channel: Full Domain
Problem Definition:
The problem discussed in earlier section is solved as a full channel as shown in the Fig. 1.1. Now there are two solid zones and one fluid zone. So there are total three zones in this case.
After solving with three zone, isotherms are shown in Fig. 2.1 which is same as the half channel solution. The variation of temperature along the interface is shown in full channel and the interface temperature is compared with the Hribersek and Kuhn [1] and also with the results of half channel as shown in the Fig. 2.2.
In addition to the comparison of interface temperature the temperature profile for the cross-section at x = 4.9 and x = 9.9 is also compared with the result of Hribersek and Kuhn [1] as shown in the Fig. 2.3.
In addition to the comparison of interface temperature the temperature profile for the cross-section at x = 4.9 and x = 9.9 is also compared with the result of Hribersek and Kuhn [1] as shown in the Fig. 2.3.
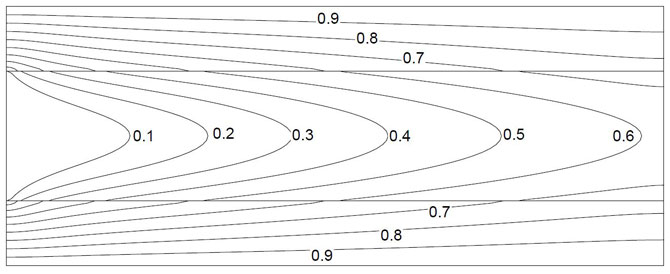
Figure 2.1: Isotherms
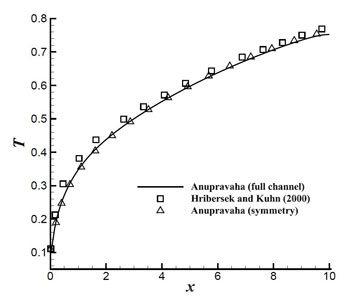
Figure 2.2: Temperature variation along the interface
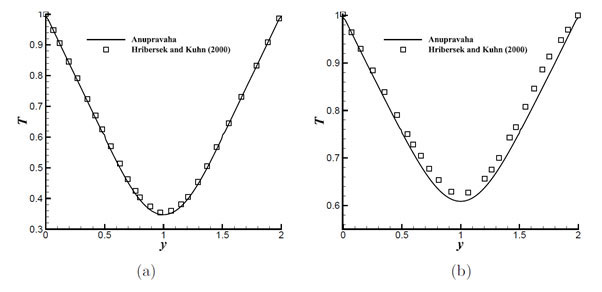
Figure 2.3: Temperature profile for cross-sections at (a) x = 4.9 (b) x = 9.9
[1] Hribersek M. and Kuhn G. (2000) ‘Conjugate heat transfer by boundary-domain integral method’, Engineering Analysis with Boundary Elements,vol. 24, pp. 297–305.


