MODULES
Gas-Droplet Flows
Problem Definition:
The assumed evaporation model is classical evaporation model by Spalding [32]. It is the simplest of all the evaporation model available having the assumption that thermal diffusivity of the droplet is infinite. This model is also known as rapid mixing model or infinite conductivity model. This model assumes that temperature within the droplet is spatially uniform although time varying. It is assumed that a two way coupling for momentum and one way coupling for temperature i.e., we are not solving for gas temperature, gas temperature is not effected by droplet evaporation.
All results of evaporation model validation are of single isolated stationary/moving droplet evaporating in a quiescent environment. For stationary droplets the evaporation is due to temperature difference only but evaporation is also dependent on the properties of the droplet and gas phase, initial droplet diameter and if convection is there then also dependent on the velocities. During unsteady evaporation droplet attains its saturation temperature and later on steady state evaporation which comprises of constant temperature droplet diameter decrease. Here the evaporation model is validated for n-heptane droplets. The validation of the evaporation model is done on the following geometry. A uniform hexahedral grid of 1600 cells has been used to mesh the flow domain. Other problem parameters are

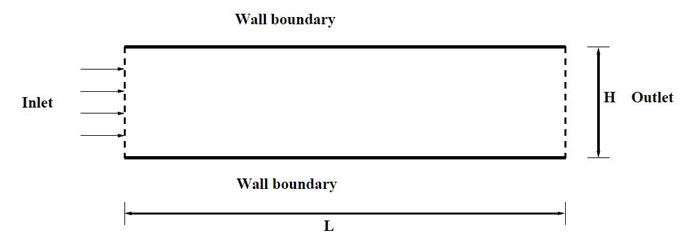
Figure 2.1: The schematic diagram of the physical domain.
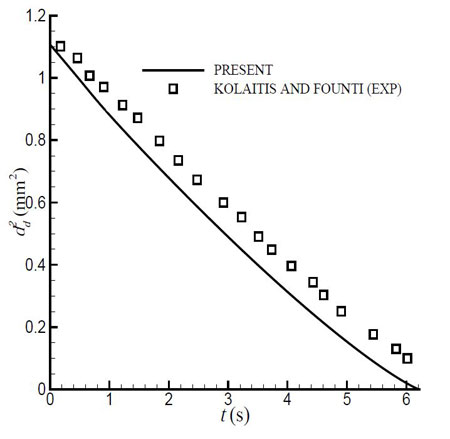
Figure 2.2: Change in diameter with time for initial droplet diameter dd=1.052 mm
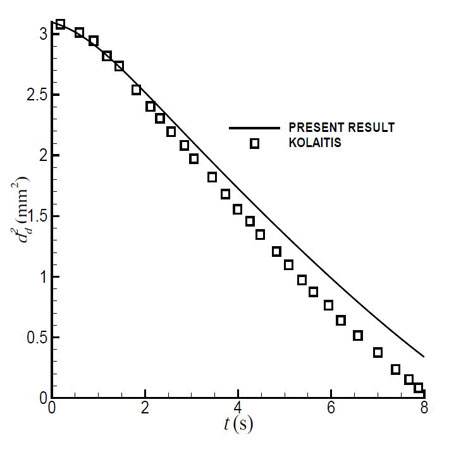
Figure 2.3: Change in diameter with time for initial droplet diameter d0=1.76 mm


