MODULES
Hartmann Flow with Conducting Walls
Hartmann Flow:
The electrical conductivity of the wall plays an important role in determining the Lorentz force. For conducting walls, the current closes its path through the walls of the channel as well as through the fluid. Therefore, the perfectly conducting wall (Cw = ∞) allows strong currents to form and the fluid has strong Lorentz forces which change the flow profile significantly. Boundary condition given to solve this problem is as flows:
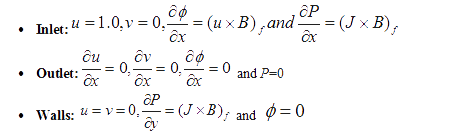
It is seen from Fig. 1.2, that the velocity decreases with increase in the strength of the applied magnetic field (i.e., increase of Hartmann number). In the core region of the channel we see a flatter velocity profile which becomes zero at the walls.
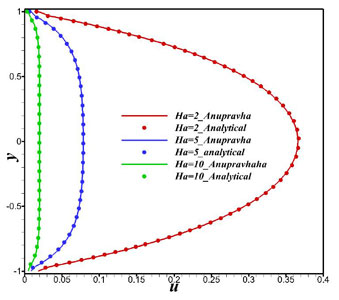
Figure 1.2: Comparison of velocity profile at outlet with analytical result at different Hartmann numbers in a channel with perfectly conducting walls.
[1] Hartmann J. and Lazarus F. (1937) ‘Experimental investigations on the flow of mercury in a homogeneous magnetic field’, Mathematisk-fysiske Meddlelser, vol. XV(7).
[2] Chang C. and Lundgren T. (1961) ‘Duct flow in magnetohydrodynamics’,
Zeitschrift fr angewandte Mathematik und Physik, vol. XII, pp. 100–114.
[3] Hughes M., Pericleous K.A., and Cross M. ‘The CFD analysis of simple
parabolic and elliptic MHD flows’, Centre for Numerical Modelling and ProcessAnalysis, University of Greenwich, London, UK.


