MODULES
Hartmann Flow with Insulating Walls
Problem Definition
In the case of insulating walls, the current closes its path through only the fluid (Hartmann layer primarily). Hence, the current strength and the Lorentz force dueto the interaction of the current and the magnetic field is weak. Therefore, it has less effect on the velocity profile as compared to the perfectly conducting walls. The results shown here are plotted at the outlet of the computational domain. Boundary condition given to solve this problem is as flows:

Orthogonal grid results
It is seen from Fig. 1.2, that the velocity decreases with increase in the strength of the applied magnetic field (i.e., increase of Hartmann number). In the core region of the channel we see a flatter velocity profile which becomes zero at the walls.
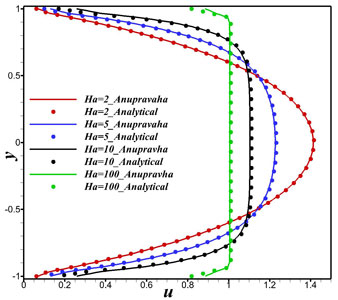
Figure 1.3: Comparison of velocity profile at outlet with analytical result at different Hartmann numbers in a channel with perfectly insulating walls for orthogonal grid.
From Fig. 1.4, we see an exact match with analytical results obtained by Chang and Lundgren [2]. And the maximum velocities are compared with M.Hughes et al [3] in the Table 1.1 and the values obtained are closer to analytical than the values given in paper. It is also seen that, for the same Hartmann number, the velocity has significantly higher values in the case of the insulating wall over the perfectly conducting walls, for all non-zero Hartmann numbers.
Table 1.1: Comparison of maximum velocities at different Hartmann numbers in a channel with perfectly insulating walls.

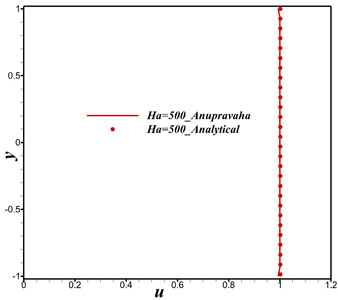
Figure 1.4: Comparison of velocity profile at outlet with analytical result at Ha=500 in a channel with perfectly insulating walls for orthogonal grid.
The results obtained for the non-orthogonal grid are compared with the results of orthogonal grid in the Fig. 1.5 and there is exact match of the results for with orthogonal grid results.
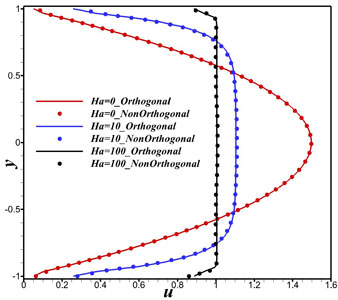
Figure 1.5: Comparison of velocity profile at outlet with analytical result at different Hartmann numbers in a channel with perfectly insulating walls for non- orthogonal grid
[1] Hartmann J. and Lazarus F. (1937) ‘Experimental investigations on the flow of mercury in a homogeneous magnetic field’, Mathematisk-fysiske Meddlelser, vol. XV(7).
[2] Chang C. and Lundgren T. (1961) ‘Duct flow in magnetohydrodynamics’,
Zeitschrift fr angewandte Mathematik und Physik, vol. XII, pp. 100–114.
[3] Hughes M., Pericleous K.A., and Cross M. ‘The CFD analysis of simple
parabolic and elliptic MHD flows’, Centre for Numerical Modelling and ProcessAnalysis, University of Greenwich, London, UK.
Website Designed and Maintained by Nidhi Sharma


