Magnetohydrodynamics Flows

The results obtained from the simulation of code are validated using different sets of problems and the results have been discussed in this chapter.

Hartmann Flow:

Hartmann flow is described as the flow of a conducting fluid between two parallel plates with an applied magnetic field orthogonal to the fluid flow. It was first theoretically and experimentally investigated by Hartmann [1]. We consider the fluid flow in the X direction driven by the pressure gradient and a constant magnetic field is applied along the Y axis as depicted in Fig. 1.1.
The walls of the channel parallel to the X Y plane shown are far and hence the flow can be treated as 2-D. The fluid with a uniform velocity enters at the inlet. The inlet velocity is calculated by integrating the analytical solution across the channel cross-section. Some distance from the entrance, the flow becomes fully developed and the velocity u depends only on the coordinate Y.

The following parameters are used for simulation.

• Length of the channel = 20
• Width of the channel = 2
• Grid points are 161× 61.
• Inlet velocity = 1 m/s
• Outlet pressure = 0 Pa

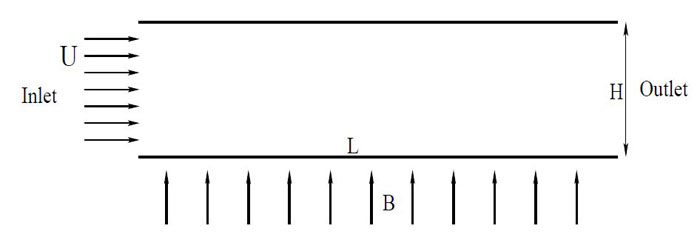
Figure 1.1: A schematic of Hartmann flow

The analytical solution of Hartmann flow is obtained by Chang and Lundgren [43] is

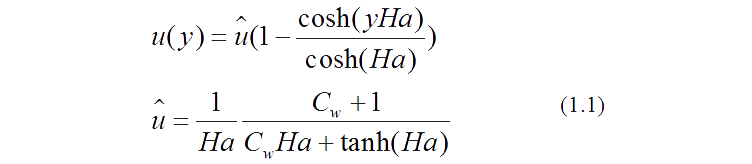
where Cw is the wall conductance ratio which is defined as the ratio of the product of electrical conductivity of wall, σw , and thickness of the wall, tw , to the product of electrical conductivity of fluid, σf , and the characteristics length, L, i.e. . The wall conductance ratios, Cw = 0 and Cw = 1 represent electrically perfectly insulating walls and perfectly conducting walls, respectively. Ha is the dimensionless parameter which measures the strength of the magnetic field and is given by

where B0 is the applied magnetic field and μ is the viscosity of the fluid.