MODULES
Natural Convection In 3-D Differentially Heated Cavity
Problem Definition:
The problem considers the laminar flow in a cubical enclosure driven by natural convection where two opposite walls (left and right) are heated differentially. The other four walls are kept perfectly insulated as shown in the figure below. The fluid inside the cavity is considered to be air with Prandtl number 0.7. We choose length of the cavity to be unity. Other quantities are acceleration due to gravity (g)=1; co-efficient of volume expansion (β)=1, specific heat (Cp)=1 and density (ρ)=1. The values of thermal conductivity (k) and dynamic viscosity (μ) are calculated from:
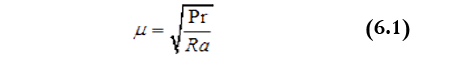

Where Ra and Pr are Rayleigh and Prandtl number. This problem has been solved by various researchers and results of these studies may be found in [1], [2].

Figure 6.1: Differentially heated cavity
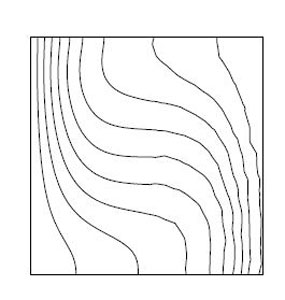
(a)
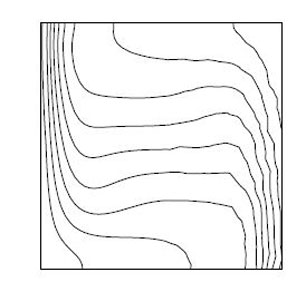
(b)
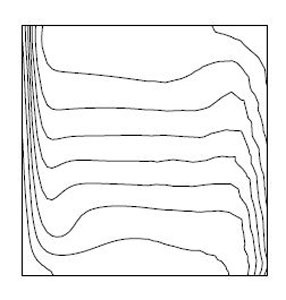
(c)
Figure 6.2: Isotherms, (a) Ra=104, (b) Ra=105, (c) Ra=106
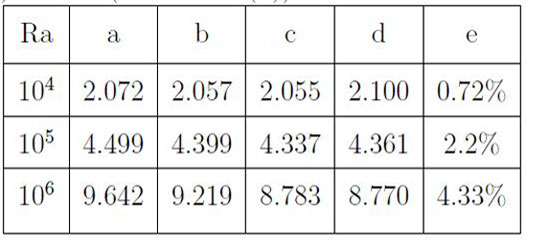
Table 6.1 shows the comparison of maximum Nusselt number values obtained in the present case with published results which shows a reasonably good match.
Table 6.1: A comparison of average Nusselt number values (a) present solution, (b) Bennett and Hsueh (non-uniform) [1], (c) Bennett and Hsueh (uniform) [1], (d)Fusegi et al. [2], (e) %error (relative to (b))
[1] Bennet B.A.V. and Hsueh J. (2006) ‘Natural convection in a cubical cavity: Implicit numerical solution of two benchmark problems’, Numerical Heat Transfer A, vol. 50, pp. 99–123.
[2] Fusegi T., Hyun J.M., Kuwahara K., and Farouk B. (1991) ‘A numerical study of three-dimensional natural convection in a differntially heated cubic cavity enclosure’, International Journal of Heat and Mass Transfer, vol. 34, pp. 1543–1557.


