MODULES
3-D Lid Driven Cavity
Problem Definition:
The problem considers the laminar flow in a cubical enclosure of dimension 1X1X1 in which the lid is driven by a constant velocity u = 1 as shown in the figure below. The length of the cavity is considered to be unity and density (ρ) =1. The value of dynamic viscosity (μ) is calculated from
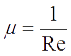
However, the computation has been carried out in a 1X1X0.5 domain where at z = 0.5, a symmetrical plane has been considered.
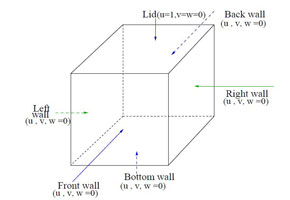
Figure 2.1: A cubical enclosure
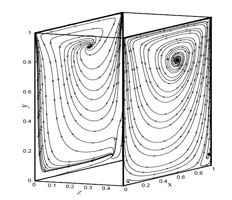
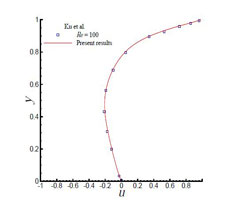
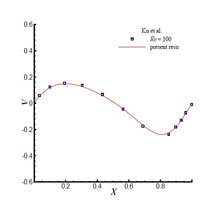
Figure 2.2: Streamlines at z=0 and z=0.5 (a) (b)
Figure 2.3: (a) u velocity along vertical centreline (b) v velocity vector along
horizontal centreline
[1] Ku H.C., Hirish R.C., and Taylor T. (1987) ‘A Pseudospectral Method for Solution of the Three-Dimensional Incompressible Navier-Stokes Equation’, Journal of Computational Physics, Vol. 70, pp. 439–462.


