My principle area of interest is Computational methods for Incompressible flows and turbulent flows. Here is a brief review of the topics that I am currently working on

Towards self-propelled regime for a finite wing : A streamlined wing subject to left-to-right flow exhibits negative drag at a specified range of pitching frequencies. This is a desired situation as the wing is now propelled by its own wake. If a cross-stream heaving is added, the combined motion makes the wake more complex and revealing. Currently we are studying the effect of heaving frequencies and phase difference beoween two side-by-side teardrop aerofoil. Particle visualization of four increasing heaving frequencies are shown below. The near wake clearly shows wake deflection, vortex merging and a few more complex issues.

 

Vortex induced vibration of a spinning sphere :Wake behind a spinning sphere exhibits fundamentally different vortical structures that have been linked to wake transition and hysteresis. When the sphere rotates axially, at smaller rotation rate helical structures cause significant spanwise vibration. However, as the rotation rate increases, unstable horseshoe vortices are observed to limit VIB in the x-y plane.



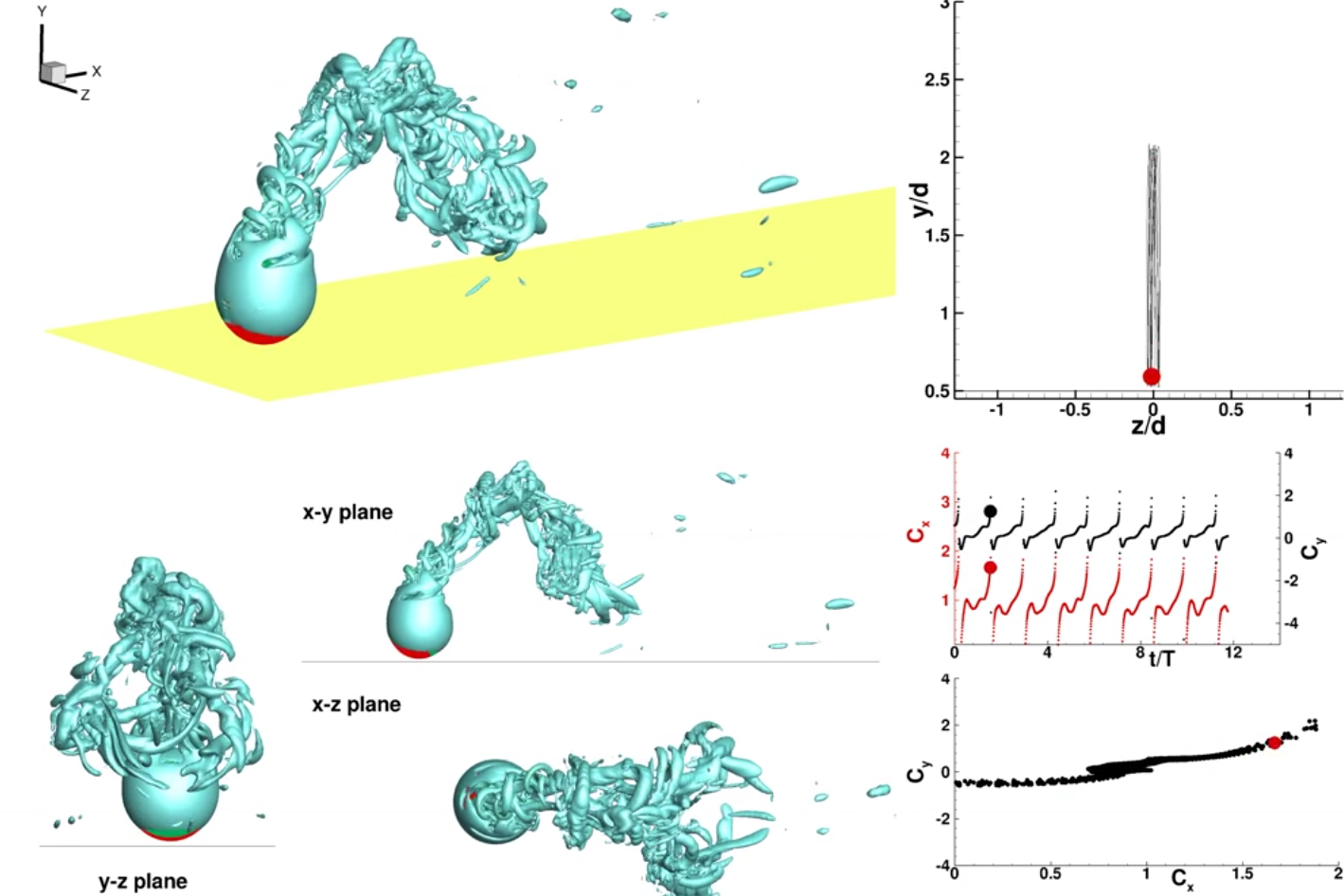
In the absence of rotation, the wake appears symmetric while the sphere follows a near-circle trajectory in the x=c plane. The wake appears identically same in the horizontal (y=0) and vertical (z=0) plane. The wake spread in the spanwise direction is even without any bias, highlighting flow irregularities are yet to set in.

Rayleigh-Benard convection : Themo-convective instability in a bottom heated configuration is one of the fundamental topic in turbulent convection. Large-scale motion, Ra-number scaling and sustenance of turbulence via production due to buoyancy are especially a few attractive features. A orderly mean flow amidst the chaos is what is intrigued many, popularly known as the "mean wind". A 3D DNS of RBF in a cubic box at Ra=10⁹ is shown below. Clearly the emerging violent plume formation has a bias to orient itself along a diagonal which causes the mean wind to sustain along it for a longer duration.



The Nu-Ra scaling law that determines the heat transfer rate is studied closely in search of a higher exponent. Asymptotic theory predicts the exponent can, in the limit, reach 1/2 which is known as the sought after "ultimate regime in thermal convection". In view of natural terrain, turbulent convection on a rough surface is studied in search of attainment of higher heat transfer. Though it is possible to achieve a higher Nu-Ra exponent with a rough surface, the dynamics of coherent structures, such as boundary layer, plume, mean wind shows significant alteration. Comparsion between a smooth and randomly rough surface RBF in a 2:1 aspect ratio box at Ra=10⁹ shows a number of interesting issues.

Vortex induced vibration with rigid body collision : VIB of a cylinder in the wake of an upstream cylinder shows a modulated behavior. However, realistically, when they are allowed to undergo rigid body collision, wake dynamics becomes rich, unpredictable and yet to be explored. We have used a penalty based collision model where the repulsive force betrween two vibrating objects springs into action once they come closer than a threshold. The repulsive force, by design, surges exponentially, preventing the objects penetrate into each other.

We observe the cylinders show "sticking", "embracing" and "colliding" tendency at different U^* (read natural frequency). Two cases depicting a dynamically changing behavior at U^*=5 and U^*=15 are shown below



At an U^* when VIB is maximum, a heavier cylinder collides violently, leading to a regular trajectory. However, lighter cylinders only appraoch theselves with the shear layer between them causing repulsion among them. It can be seen from the streak visualization at m^*=1 (left) and m^*=10 (right)

Magnus effect on a spinning sphere near a wall : When a sphere rotates near a wall, in addition to the axis of rotation, effect of boundary layer and collision with the wall have a decisive influence on the magnus lift on the sphere. Further, structural response of the sphere with U^* is not the same at all Reynolds number. Thus, a complex combination of boundary layer separation and wake transition becomes an essential study to understand the sideways movement of the sphere. Spinning and swinging of a cricket ball has a direct connotaion with this problem. Consider rotation about the z-axis. At Re=500, shear layer separation on the sphere breaks the horshoe structures with VIB being suppressed



However, at Re=1000, a sharp deflection of the separated trail of small scale vortices is observed. Violent collision and large scale wake deflection causes intense vibration of the sphere which hardly moves sideways.